Duck Tales Inflation Lesson

Hayek vs. Keynes

A rap demonstrating the differences between Keynesian and Austrian schools of economics in general, and particularly as they relate to the recent financial crisis and the recession.

Farm Subsidies and Sustainable Agriculture

I  ran across a piece by the EWG titled 'Government's Continued Bailout of Corporate Agriculture' which, in addition to the title, made some pretty bold and possibly misleading statements. I'm not saying this is intentional on the part of EWG, but these statements could easily be misinterpreted.

From 1995-2009 the largest and wealthiest top 10 percent of farm program recipients received 74 percent of all farm subsidies

This is true, but it could give the false perception that farm subsidies benefit large farms perhaps at the expense of smaller farms, but I addressed this before in another post Do Farm Subsidies Benefit the Largest Farms the Most?

It's true that many subsidies are tied to commodity production. As a result, those that grow more commodities (i.e. larger farms) will get more money from the government. As a result larger producers take in a larger share of all subsidies (especially those related to commodities). However, subsidies account for a much smaller percentage of income for large producers, and make up a much larger percentage of total income for medium or small producers.  

EWG  does admit that they favor subsidies going to smaller and midsize farms, where they have the biggest impact on operating budgets.  Another quote:


The vast majority of farm subsidies go to raw material for our industrialized food system, not the foods we actually eat. Even less money goes to support the production of the fruits and vegetables that are the foundation of a healthy diet.


This couldn't be further from the truth. It is true, as I discussed above, that most of the subsidies go to commodities, but it isn't true that they don't contribute to the production of foods that we actually eat. In fact, as Michael Pollan has brilliantly stated:

"What I keep finding in case after case, if you follow the food back to the farm — if you follow the nutrients, if you follow the carbon — you end up in a corn field in Iowa, over and over and over again." -Michael  Pollan

It is a miracle that modern sustainable agriculture can feed so many people in so many ways, with just a few common staple crops, and do it sustainably!

The EWG quote also could give some people the perception that healthy supplements in our diets, like fruits and vegetables, are more expensive than processed foods containing corn and soybeans because corn and soybeans are subsidized more heavily than fruits and vegetables. Again, this couldn't be further than the truth. The agronomics, labor, risk, economies of scale, and capital costs associated with fruit and vegetable production make those crops much more expensive than commodities, and have a much larger role on their prices than subsidies.  Eliminating commodity programs would have an insignificant impact at the retail level, and the subsides required to make fruits and vegetables more affordable would dwarf what we are currently spending on commodities. 

Finally, while this corporate giveaway has gone on unabated, conservation continues to be shortchanged.

While this may be true, in terms of the allocation of funds, conservation and sustainability in terms of on the farm practices isn't shortchanged in the least. Market forces have overcome subsidy related distortions and led producers and agribusinesses to focus heavily on green technologies including herbicide and pest resistance, water use efficiency, fuel efficiency etc.  Again, all the practices that make modern agriculture, sustainable agriculture.

Modern Sustainable Agriculture

Economic Growth and Technological Change: Biotechnology and Sustainability

In class we spoke of the impact that technological change can have on economic growth, and we viewed the following video regarding biotechnology:



You can find an additional video regarding technological change in beef production and its impact on sustainability here:  Feedlot Cattle are Most 'Green.'




 This report from the UN's Economic Commission for Africa: "Harnessing Technologies for Sustainable Development"  highlights (especially in Ch 3) the impacts of biotechnology on economic growth and sustainability in developing nations.

Most recently, research from the journal Science provides examples of positive externalities or 'spillover' effects from biotech corn to non-biotech  farmers.

Below is a listing of peer reviewed articles related to the impacts of biotechnology on productivity and sustainability in agriculture.

It would be extremely biased to present to you the claim that biotechnology is the panacea for sustainable economic growth, however it certainly provides a great example of how technological change can improve productivity and lead to economic growth.

Related Research:

The environmental impact of dairy production: 1944 compared with 2007. Journal of Animal Science,Capper, J. L., Cady, R. A., Bauman, D. E. 2009; 87 (6): 2160 DOI: 10.2527/jas.2009-1781

-reduced carbon footprint in dairy production

Communal Benefits of Transgenic Corn. Bruce E. Tabashnik  Science 8 October 2010:Vol. 330. no. 6001, pp. 189 - 190DOI: 10.1126/science.1196864


"Bt corn planted near non-Bt corn can provide the unmodified plants with indirect protection from pests"


“Antimicrobial Resistance: Implications for the Food System.” Doyle et al., Institute of Food Technologists
Comprehensive Reviews in Food Science and Food Safety, Vol.5, Issue 3, 2006ter for Molecular

-safety of pharmaceutical technologies in food production in relation to antibiotic use in livestock

"Microbiological Quality of Ground Beef From Conventionally-Reared Cattle and "Raised without Antibiotics" Label Claims" Journal of Food Protection, July 2004,Vol 67 Issue 7 p. 1433-1437

-factors other than the sub therapeutic use of antibiotics in beef production contribute to antimicrobial resistant bacteria in ground beef

San Diego Center for Molecular Agriculture: Foods from Genetically Modified Crops ( pdf)

-summary of environmental and health benefits of biotechnology

‘‘Hybrid Corn.’’ Abelson, P.H. (1990) Science 249 (August 24): 837. -improved diversity of crops planted

Enterprise and Biodiversity: Do Market Forces Yield Diversity of Life? David Schap and Andrew T. Young Cato Journal, Vol. 19, No. 1  (Spring/Summer 1999)

-improved diversity of crops planted

A Meta-Analysis of Effects of Bt Cotton and Maize on Nontarget Invertebrates. Michelle Marvier, Chanel McCreedy, James Regetz, Peter Kareiva Science 8 June 2007: Vol. 316. no. 5830, pp. 1475 – 1477

-reduced impact on biodiversity

‘‘Diversity of United States Hybrid Maize Germplasm as Revealed by Restriction Fragment Length Polymorphisms.’’ Smith, J.S.C.; Smith, O.S.; Wright, S.; Wall, S.J.; and Walton, M. (1992) Crop Science 32: 598–604

-improved diversity of crops planted

Comparison of Fumonisin Concentrations in Kernels of Transgenic Bt Maize Hybrids and Nontransgenic Hybrids. Munkvold, G.P. et al . Plant Disease 83, 130-138 1999.

-Improved safety and reduced carcinogens in biotech crops

Indirect Reduction of Ear Molds and Associated Mycotoxins in Bacillus thuringiensis Corn Under Controlled and Open Field Conditions: Utility and Limitations. Dowd, J. Economic Entomology. 93 1669-1679 2000.

-Improved safety and reduced carcinogens in biotech crops

“Why Spurning Biotech Food Has Become a Liability.’' Miller, Henry I, Conko, Gregory, & Drew L. Kershe. Nature Biotechnology Volume 24 Number 9 September 2006.

-Health and environmental benefits of biotechnology

Genetically Engineered Crops: Has Adoption Reduced Pesticide Use? Agricultural Outlook ERS/USDA Aug 2000

-environmental benefits and reduced pesticide use of biotech crops

GM crops: global socio-economic and environmental impacts 1996- 2007. Brookes & Barfoot PG Economics report

-environmentalbenefits of biotech: reduced pollution, improved safety, reduced carbon footprint

Soil Fertility and Biodiversity in Organic Farming. Science 31 May 2002: Vol. 296. no. 5573, pp. 1694 – 1697 DOI: 10.1126/science.1071148

-20% lower yields in non-biotech organic foods

‘Association of farm management practices with risk of Escherichia coli contamination in pre- harvest produce grown in Minnesota and Wisconsin.’ International Journal of Food Microbiology Volume 120, Issue 3, 15 December 2007, Pages 296-302

-comparison of E.Coli risks and modern vs. organic food production methods, odds of contamination are 13x greater for organic production

The Environmental Safety and Benefits of Growth Enhancing Pharmaceutical Technologies in Beef Production. By Alex Avery and Dennis Avery, Hudson Institute, Centre for Global Food Issues.

-Grain feeding combined with growth promotants also results in a nearly 40 percent reduction in greenhouse gases (GHGs) per pound of beef compared to grass feeding (excluding nitrous oxides), with growth promotants accounting for fully 25 percent of the emissions reductions- see also: Organic, Natural and Grass-Fed Beef: Profitability and constraints to Production in the Midwestern U.S. Nicolas Acevedo John D. Lawrence Margaret Smith August, 2006. Leopold Center for Sustainable Agriculture)

Lessons from the Danish Ban on Feed Grade Antibiotics. Dermot J. Hayes and Helen H. Jenson. Choices 3Q. 2003. American Agricultural Economics Association.

-Ban on feed grade sub- therapeutic antibiotics lead to increased reliance on therapeutic antibiotics important to human health.

Does Local Production Improve Environmental and Health Outcomes. Steven Sexton. Agricultural and Resource Economics Update, Vol 13 No 2 Nov/Dec 2009. University of California.

-local production offers no benefits to sustainability


Greenhouse gas mitigation by agricultural intensification Jennifer A. Burneya,Steven J. Davisc, and David B. Lobella.PNAS  June 29, 2010   vol. 107  no. 26  12052-12057

-'industrial agriculture' aka family farms utilizing modern production technology have a mitigating effect on climate change

Clearing the Air: Livestock's Contribution to Climate ChangeMaurice E. Pitesky*, Kimberly R. Stackhouse† and Frank M. MitloehnerAdvances in Agronomy Volume 103, 2009, Pages 1-40

-transportation accounts for at least 26% of total anthropogenic GHG emissions compared to roughly 5.8% for all of agriculture & less than 3% associated with livestock production vs. 18% wrongly attributed to livestock by the FAO report 'Livestock's Long Shadow' Conclusion: intensified 'modern' livestock production is consistent with a long term sustainable production strategy

Large Agriculture Improves Rural Iowa Communities
http://www.soc.iastate.edu/newsletter/sapp.html

-"favorable effect of large-scale agriculture on quality of life in the 99 Iowa communities we studied"

Comparing the Structure, Size, and Performance of Local and Mainstream FoodSupply Chains
Robert P. King, Michael S. Hand, Gigi DiGiacomo,Kate Clancy, Miguel I. Gómez, Shermain D. Hardesty,Larry Lev, and Edward W. McLaughlin
Economic Research Report Number 99 June 2010
http://www.ers.usda.gov/Publications/ERR99/ERR99.pdf

-Study finds that fuel use per cwt for local food production was 2.18 gallons vs. .69 and 1.92 for intermediate and traditional supply chains for beef

The Constutution, Public Choice and Democracy

There are certainly differences between the ways that markets allocate resources ( using prices which reflect trade-offs based on the knowledge and preferences of millions of individuals) vs government (which allocates resources using command and control based on the more limited knowledge and preferences of a few voters, elected officials, or appointed bureaucrats).

The economic analysis of political institutions represents a sub field of economics referred to as 'Public Choice Economics.' The following link will take you to an article 'The Public Choice Revolution', Regulation Fall 2004.

This article summarizes some of the major findings from the field of public choice. The article discusses among many things, why do we need government, and what are the tradeoffs between tyranny (or Leviathan ) and anarchy.

"Once it is admitted that the state is necessary, positive public choice analyzes how it assumes its missions of allocative efficiency and redistribution. Normative public choice tries to identify institutions conducive to individuals getting from the state what they want without being exploited by it."

Another section looks at the analysis of voting. It discusses problems with using voting to allocate resources, such as cycling and the median voter theorem. It also looks at issues related to special interests, bureaucracies, and the role of representative government in democratic systems.

"In our democracies, voters do not decide most issues directly. In some instances, they vote for representatives who reach decisions in parliamentary assemblies or committees. In other instances, they elect representatives who hire bureaucrats to make decisions. The complexity of the system and the incentives of its actors do not necessarily make collective choices more representative of the citizens’ preferences."

Particularly the article looks at how more government with a larger budget leads to more power for special interests:

"Interest groups will engage in what public choice theorists call “rent seeking,” i.e., the search for redistributive benefits at the expense of others. The larger the state and the more benefits it can confer, the more rent-seeking will occur. “The entire federal budget,” writes Mueller, “can be viewed as a gigantic rent up for grabs for those who can exert the most political muscle.”

The moral of the public choice story is that democracy and governments are not perfect. When we have issues with market outcomes and we are thinking about new regulations or government spending to correct those problems, public choice analysis offers a guide. Public choice analysis implies that we have to question which system will provide the best information and incentives to act on that information to achieve the results that we want. The U.S. Consittution with its separation of powers and the specifically enumerated powers in Article 1 Section 8 provides a framework for achieving this balance. The democratic process itself offers no guarantee that the decision will be the best solution to our problems.

Markets and Knowledge- with Applications to Disaster Relief

I Pencil -The actual essay starts on page 4 within the document (actually page 8 in the pdf) This discusses the role that prices play in conveying knowledge and directing and organizing behavior in society- often described as a ‘spontaneous order.’


Economics has many applications outside of what you may stereotypically have in mind. Besides giving insight into how to run a business, economic principles apply to other areas of human behavior, like for instance, disaster response:

The Use of Knowledge in Disaster Relief Management


Government’s Response to Hurricane Katrina: A public choice analysis


Again, these are really upper level applications of basic principles of economics. Don’t feel overwhelmed by the material. Just scan through and try to get a general idea. What we will cover in class will be much more basic. However, these are great examples of applications of the principles we will talk about in class.

Using R

Many people that are involved in data analysis may have one software package that they prefer to use, but may never have heard of R, or even thought about trying something new. R is a statistical programming language with a command line interface that is becoming more and more popular every day. If you are used to a point and click interface (like SPSS or Excel for example) the learning curve for R may be quite steep but well worth the effort. If you are already familiar with a programming language, like SAS for instance, (SPSS also has a command line interface) the switch to R may not be that difficult but could be very rewarding. In fact there is a free version of a reference available entitled ‘R for SAS and SPSS Users’ that I found very helpful getting started.

How I use R

I often use SAS for data management, recoding, merging and sub-setting data sets, and cleaning and formatting data. I’m getting better at doing some of these things in R but I just have more experience in SAS. I first became interested in using R for spatial lag models and geographically weighted regression, which requires the construction of spatial weights matrices. (These techniques aren't as straight forward if at all possible in SAS). I've also used R for data visualization, data mining/machine learning, as well as social network analysis. I give my students the option to use R in the statistics course I teach and I have had several pursue it. And most recently, I have become acquainted with SAS IML Studio, which is a product that will better enable me to integrate some of my SAS related projects with some of the powerful tools R provides.

How can you use R?

Google’s Chief Economist Hal Varian uses R . His paper Predicting the Present with Google Trends is a great example of how R can be used for prediction, and is loaded with R code and graphics. Facebook uses R as well:

“Facebook’s Data Team used R in 2007 to answer two questions about new users: (i) which data points predict whether a user will stay? and (ii) if they stay, which data points predict how active they’ll be after three months?” (Link- how Google and Facebook are using r by Michael E. Driscoll at Dataspora.com)

The New York Times recently did a feature on R entitled ‘Data Analysts Captivated by R’ where industry leaders explain why and how they use R.

“Companies like Google and Pfizer say they use the software for just about anything they can. Google, for example, taps R for help understanding trends in ad pricing and for illuminating patterns in the search data it collects. Pfizer has created customized packages for R…Companies as diverse as Google, Pfizer, Merck, Bank of America, the InterContinental Hotels Group and Shell use it.”

The article goes on to discuss the proliferate and diverse packages offered by R:

“One package, called BiodiversityR, offers a graphical interface aimed at making calculations of environmental trends easier. Another package, called Emu, analyzes speech patterns, while GenABEL is used to study the human genome. The financial services community has demonstrated a particular affinity for R; dozens of packages exist for derivatives analysis alone.”

In a recent issue of Forbes (Power in the Numbers by Quentin Hardy May 2010) R is discussed as a powerful analysis tool as well as its potential to revolutionize business, markets, and government:

‘Using an R package originally for ecological science, a human rights group called Benetech was able to establish a pattern of genocide in Guatemala. A baseball fan in West Virginia used another R package to predict when pitchers would get tired, winning himself a job with the Tampa Bay Rays. An R promoter in San Francisco, Michael Driscoll, used it to prove that you are seven times as likely to change cell phone providers the month after a friend does. Now he uses it for the pricing and placement of Internet ads, looking at 100,000 variables a second”

“Nie posits that statisticians can act as watchdogs for the common man, helping people find new ways to unite and escape top-down manipulation from governments, media or big business...It's a great power equalizer, a Magna Carta for the devolution of analytic rights… "

The proprietary adaptation of R, Revolution R was recently discussed on Fox Business; you can see the interview here.

A good way to get a look at what researchers are doing with R would be to review presentation topics at a past UseR conference, from 2008:


Andrew Gelman, Bayesian generalized linear models and an appropriate default prior

Michael Höhle, Modelling and surveillance of infectious diseases - or why there is an R in SARS

E. James Harner, Dajie Luo, Jun Tan, JavaStat: a Java-based R Front-end

Robert Ferstl, Josef Hayden, Hedging interest rate risk with the dynamic Nelson/Siegel model

Jacob Michaelson, Andreas Beyer, Random Forests for eQTL Analysis: A Performance Comparison

Graham J. WilliamsDeploying , Data Mining in Government - Experiences With R/Rattle

Jing Hua Zhao, Qihua Tan, Shengxu Li, Jian'an LuanSome, Perspectives of Graphical Methods for Genetic Data

Who else uses R?

A review of past participant lists from UseR also gives you a pretty good idea about companies that are using R. Past participants includes:

Merril Lynch, Merck Research Laboratories , Siemens AG,, BASF SE, Astra Zeneca, Bayer CropScience, Novartis Pharma, AT&T Labs, Bell Labs, Bank of Canada, Credit Suisse, Max Planck Institute, US Naval Academy, Harvard, Vanderbilt University + many universities.

UCLA has great online resources for R and Stanford offers a course called Elements of Statistical Learning which utilizes a textbook with the same title that heavily references R code.


Downloading and using R

For more information about R and to download it to try it yourself, the place to start is the R Project website: http://www.r-project.org/

A few other great references for R can be found here:

Quick R (Statistics Guide)- http://www.statmethods.net/index.html

Revolution Analytics- (Blog) - http://blog.revolutionanalytics.com/

http://www.r-bloggers.com/

Facebook- R Bloggers Group
Statistical Computing with R: A Tutorial (Illinois State University) –

http://math.illinoisstate.edu/dhkim/rstuff/rtutor.html(UCLA R Class Notes) -great example code for getting started with R –
http://www.ats.ucla.edu/stat/R/notes/Using R for Introductory Statistics (John Verzani) - http://cran.r-project.org/doc/contrib/Verzani-SimpleR.pdf


References:

Changing the Face of Analytics. Fox Business Network via YouTube: http://www.youtube.com/watch?v=4nOMhTBuXl8&feature=youtube_gdata

Data Analysts Captivated by R’s Power. New York Times. January 6, 2009.

Driscoll, Michael E. How Google and Facebook Are Using R. Dataspora Blog. February 19, 2009. http://dataspora.com/blog/predictive-analytics-using-r/

Hardy, Quentin. Power in Numbers. Forbes Magazine. May 24,2010.

Hastie, Tibshirani, and Friedman. The Elements of Statistical Learning. Second Edition. February 2009. http://www-stat.stanford.edu/~tibs/ElemStatLearn/

Hyunyoung Choi and Hal Varian. Predicting the Present with Google Trends. Google Inc.
Draft Date April 10, 2009. http://static.googleusercontent.com/external_content/untrusted_dlcp/www.google.com/en/us/googleblogs/pdfs/google_predicting_the_present.pdf

R 4stats.com: http://rforsasandspssusers.com/

The R Project: http://www.r-project.org/

UCLA Resources to Help You Learn and Use R: http://www.ats.ucla.edu/stat/R/

Kernal Density Plots

# When viewing this post the code looks messy, but just copy and paste into
# notepad or the R scripting window and it should line up

# This program is a little more complicated than the previous ones,and some of
# the topics may be a little out of the scope of this class, but if you
# are interested and don't understand something let me know


# example plots from Part 2 of the program using sample salary data:

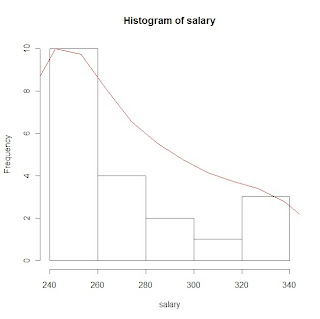
# histogram of salary data with gaussian KDE plot




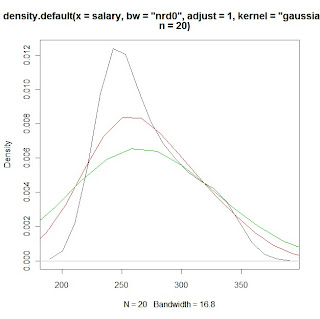
# KDE plots of salary data with varying bandwidth selections using the 'adjust'
# option







# PROGRAM NAME: KDE_R
# DATE: 6/18/2010
# AUTHOR : MATT BOGARD
# PURPOSE: EXAMPLE OF KERNAL DENSITY ESTIMATES IN R
# DATA USED: SIMULATED WITHIN SCRIPT
# PACKAGES: lattice Hmisc
# OUTPUT FILE: "C:\Documents and Settings\wkuuser\My Documents\TOOLS AND REFERENCES\R References"
# UPDATES:
#
#
# COMMENTS: GIVE A BASIC UNDERSTANDING OF THE density() FUNCTION IN R
# AND BANDWIDTH, KERNAL SELECTION, AND PLOTTING
#
# REFERENCES: ADAPTED FROM
# http://ise.tamu.edu/metrology/Group%20Seminars/Kernel_Density_Estimation_2008JUN27_2.pdf
#
# CONTENTS: PART1 EXAMPLES USING CODE GENERATED NORMALLY DISTRIBUTED DATA
# PART2 EXAMPLES USING SAMPLE DATA

#---------------------------------------------------------------#
# PART1 EXAMPLES USING CODE GENERATED NORMALLY DISTRIBUTED DATA
#---------------------------------------------------------------#

x <- seq(-4, 4, 0.01) y <- dnorm(x, mean=0, sd=1 # create x,y data set that is exactly normal

rn <- rnorm(1000, mean=0, sd=1 # create a set of random normal values

# plot the density of the random numbers you just generated
# let the bandwidth = nrd0 "rule of thub" h= .9*A*n*exp(-1.5), A = min{s,IQR/1.34}
# select the gaussian kernal using 1000 points (which you just generated)



plot(density(x=rn, bw="nrd0", kernel="gaussian", n=1000), col=5) # gaussian is default

lines(x, y) # plot the exactly normal data set you created earlier to compare



# plot a series of KDE plots with varying bandwitdth using 'width='option
# When this option is specified instead of 'bw',and is a number, the density
# function bandwidth is set to a kernel dependent multiple of 'width'

for(w in 1:3)
lines(density(x=rn, width=w, kernel="gaussian", n=1000), col=w+1)


# what if we change the kernal
# first close the graphics window to start over
# look at varius bandwidths using a kernal other than gaussian

# KDE otpions:
# gaussian rectangular triangular
# biweight cosine optcosine"
# epanechnikov


plot(density(x=rn, bw="nrd0", kernel="rectangular", n=1000), col=1)
for(w in 1:3)
lines(density(x=rn, width=w, kernel="rectangular", n=1000), col=w+1)


# or to just look at various densities in one plot
# using a lines statment specifying the specific kernal

plot(density(x=rn, bw="nrd0", kernel="gaussian", n=1000), col=1)
lines(density(x=rn, bw="nrd0", kernel="rectangular", n=1000), col=2)
lines(density(x=rn, bw="nrd0", kernel="triangular", n=1000), col=3)
lines(density(x=rn, bw="nrd0", kernel="epanechnikov", n=1000), col=4)
lines(density(x=rn, bw="nrd0", kernel="biweight", n=1000), col=5)
lines(density(x=rn, bw="nrd0", kernel="cosine", n=1000), col=6)
lines(density(x=rn, bw="nrd0", kernel="optcosine", n=1000), col=7)

# or to just look at various densities in one plot
# using a lines statment specifying the specific kernal

plot(density(x=rn, bw="nrd0", kernel="gaussian", n=1000), col=1)

# note if you want the default gaussian, it does not have to be specified

plot(density(x=rn, bw="nrd0", n=1000), col=1)


#-----------------------------------#
# PART2 EXAMPLES USING SAMPLE DATA
#-----------------------------------#

# load salary data

salary<-c(240,240,240,240,240,240,240,240,255,255,265,265,280,280,290,300,305,325,330,340)
print(salary)

library(Hmisc) # load for describe function
describe(salary) # general stats

library(lattice) # load lattice package for histogram graphics
hs <- hist(salary) # plot histogram and store data
print(hs)

# create a kde of salary data (gaussian)and store it as dens

dens <- density(x=salary, bw="nrd0", n=20)
print(dens)


rs <- max(hs$counts/max(dens$y)) # create scaling factor for plotting the density
lines(dens$x, dens$y*rs, col=2) # plot density over histogram using lines statment

# compare this to just plotting the non-rescaled density over the histogram

lines(density(x=salary, bw="nrd0", n=20),col=3) # green line barely shows up

# also, compare to just plotting the estimated density for the sample
# data in a separate plot


plot(density(x=salary, bw="nrd0", n=20)) # or equivalently
plot(dens, col=3)

# now that we understand the various ways we can plot a specified KDE
# we can apply the tools used in part 1 to look at the effects of
# various bandwidths and kernal choices - first close the graphing window

# what if we change the kernal
# first close the graphics window to start over
# look at varius KDEs

# KDE otpions:
# gaussian rectangular triangular
# biweight cosine optcosine"
# epanechnikov


# look at various densities in one plot
# using a lines statment specifying the specific kernal

plot(density(x=salary, bw="nrd0", kernel="gaussian", n=20), col=1)
lines(density(x=salary, bw="nrd0", kernel="rectangular", n=20), col=2)
lines(density(x=salary, bw="nrd0", kernel="triangular", n=20), col=3)
lines(density(x=salary, bw="nrd0", kernel="epanechnikov", n=20), col=4)
lines(density(x=salary, bw="nrd0", kernel="biweight", n=20), col=5)
lines(density(x=salary, bw="nrd0", kernel="cosine", n=20), col=6)
lines(density(x=salary, bw="nrd0", kernel="optcosine", n=20), col=7)

# what if we don't specify a bandwidth (clear graphics window)
# what is the default density

plot(density(x=salary, bw="nrd0", kernel="gaussian", n=20), col=1)
lines(density(x=salary, kernel="gaussian", n=20), col=2)# nrd0 appears to be default

# what if we change the default
# nrd (a variation of nrd0)
# ucv (unbiased cross validation)
# bcv (cross validation)

lines(density(x=salary, bw="ucv", kernel="gaussian", n=20), col=2)
lines(density(x=salary, bw="bcv", kernel="gaussian", n=20), col=3)
lines(density(x=salary, bw="nrd", kernel="gaussian", n=20), col=4)

# use print option to see how the bw value changes with each method

print(density(x=salary, bw="nrd0", kernel="gaussian", n=20))

# look at the differences in calculated
# bandwidth and plots with the adjust option

for(w in 1:3)
print(density(x=salary, bw="nrd0", adjust=w, kernel="gaussian", n=20))


plot(density(x=salary, bw="nrd0",adjust=1, kernel="gaussian", n=20), col=1)
lines(density(x=salary, bw="nrd0",adjust=2,kernel="gaussian", n=20), col=2)
lines(density(x=salary, bw="nrd0",adjust=3,kernel="gaussian", n=20), col=3)

Inference, Hypothesis Testing, & Regression

Inference: the exercise of providing information about the population based on information contained in the sample

Type 1 Error: rejecting a true null hypothesis
- the probabability of rejecting a true null hypothesis ( or the probability of a type 1 error) is equal to alpha or 'α' This is also the same as the level of significance in a hypothesis test.

Type II Error: failing to reject, or loosely speaking, 'accepting' the null hypthesis when it is false
-the probability of a type II error =beta or β

Power: the probability of rejecting the null hypothesis when it is false. (1-β)

Regression Model: describes how the dependent variable (y) is related to the independent variable (x), also known as the least squares line.

y = b0 + b1*x

This is derived by the process of least squares, which gives the value for the slope (b1) and the intercept (bo) that minimizes the sum of the squared deviations between the observed values of the dependent variable (Y) and the estimated values of the dependent variable (Y*).

Co-efficient of determination(R-squared) = SSR/SST -> gives the proportion of total variation explained by the regression model. Larger values indicate that the sample data are closer to the least squares line, or a stronger linear relationship exists.

Standard Normal Distribution & Z-values

############################################
# Below is R code for plotting normal distributions - illustrating
# the changes in the distribution when standard deviation changes.
# -selected graphics are imbedded below
#
# Also calculates area under the normal curve for given Z
#
# Finally plots 3-D bivariate normal density
#
#############################################



# PROGRAM NAME: NORMAL_PLOT_R
#
# ECON 206
#
# ORIGINAL SOURCE: The Standard Normal Distribution in R:
# http://msenux.redwoods.edu/math/R/StandardNormal.php
#
#
#
#


#PLOT NORMAL DENSISTY

x=seq(-4,4,length=200)
y=dnorm(x,mean=0,sd=1)
plot(x,y,type="l",lwd=2,col="red")

#######################################





###################################





# INCREASE THE STANDARD DEVIATION

x=seq(-4,4,length=200)
y=dnorm(x,mean=0,sd=2.5)
plot(x,y,type="l",lwd=2,col="red")


#####################################



####################################

# DECREASE THE STANDARD DEVIATION

x=seq(-4,4,length=200)
y=dnorm(x,mean=0,sd=.5)
plot(x,y,type="l",lwd=2,col="red")

# CALCULATING AREA FOR GIVEN Z-VALUES

# RECALL, FOR THE STANDARD NORMAL DISTRIBUTION THE MEAN = 0 AND
# THE STANDARD DEVIATION = 1
# THE pnorm FUNCTION GIVES THE PROBABILITY FOR THE AREA TO THE LEFT
# OF THE SPECIFIED Z-VALUE ( THE FIRST VALUE ENTERED IN THE FUNCTION)
# THE OUTPUT SHOULD MATCH WHAT YOU GET FROM THE NORMAL TABLE IN YOUR BOOK
# OR THE HANDOUT I SENT YOU

pnorm(0,mean=0, sd=1) # Z =0

pnorm(1,mean=0, sd=1) # Z <= 1

pnorm(1.55, mean=0, sd=1) # Z<=1.55

pnorm(1.645, mean=0, sd=1) # Z<= 1.645


# LETS LOOK AT A BIVARIATE NORMAL
# DISTRIBUTION


# first simulate a bivariate normal sample

library(MASS)

bivn <- mvrnorm(1000, mu = c(0, 0), Sigma = matrix(c(1, 0, 0, 1), 2))

# now we do a kernel density estimate

bivn.kde <- kde2d(bivn[,1], bivn[,2], n = 100)

# now plot your results

contour(bivn.kde)
image(bivn.kde)

persp(bivn.kde, phi = 45, theta = 30)


# fancy contour with image

image(bivn.kde); contour(bivn.kde, add = T)

# fancy perspective

persp(bivn.kde, phi = 45, theta = 30, shade = .1, border = NA)

###############################################

Regression Demo

Basic Regression in R

#
# COMMENTS: BASIC INTRODUCTION TO REGRESSION USING R
#


#
# WILLIAMS P 572 #1
#


# GET DATA

x<-c(1,2,3,4,5)

y<-c(3,7,5,11,14)


# PLOT DATA

plot(x,y)

reg1 <- lm(y~x) # COMPUTE REGRESSION ESTIMATES

summary(reg1) # PRINT OUTPUT

abline(reg1) # PLOT REGRESSION LINE



#
# SCHAUM'S P. 274 #14.2
#


#GET DATA

x<-c(20,16,34,23,27,32,18,22)
y<-c(64,61,84,70,88,92,72,77)

plot(x,y) #PLOT DATA

reg1 <- lm(y~x) # COMPUTE REGRESSION ESTIMATES

summary(reg1) # PRINT OUTPUT

abline(reg1) # PLOT REGRESSION LINE

Social Network Analysis of Tweets Using R

This past week I attended the AACRAO conference in New Orleans. This provided a great opportunity to demonstrate one of the many things you can do wit R. ( for more about the R statistical programming language see here) R is capable of many outside the box applications (beyond just the basic statistical techniques) such as social network analysis.

The image below represents the network of the last 100 tweets using the hashtag #aacrao10. The data was captured and the network was constructed using R. Thanks to Drew Conway for showing me how to do this.

(Click to enlarge)



Labeled dots indicate users that used the specified hashtag while unlabeled dots indicate 'friends' of users that used the specified hashtag.The code also allows you to compute important network metrics such as measures of centrality that are helpful in key actor analysis.

Statistics Definitions

SAMPLE POINT- each individual outcome of an experiment

SAMPLE SPACE-the collection of all possible sample points in an experiment

EVENT-a collection of sample points

PRIOR PROBABILITY-initial estimate of the probability of an event

RANDOM VARIABLE-a numerical description of the outcome of an experiment

EXPECTED VALUE OF A RANDOM VARIABLE-a measure of the average value of a random variable

VARIANCE OF A RANDOM VARIABLE-a measure of the dispersion of a random variable

PARAMETER-a numerical measure from a population

STATISTIC- a numerical measure from a sample

SAMPLING DISTRIBUTION-a probability distribution for all possible values of a statistic

PROPERTIES OF ESTIMATORS:

Unbiased: Property of a statistic where the expected value of a statistic/estimator = the parameter being estimated
Consistency: as n increases the probability that the value of a statistic/estimator gets closer to the parameter being estimated increases

CENTRAL LIMIT THEOREM-the sampling distribution of the sample mean can be approximated by a normal probability distribution as the sample size becomes large. This holds even if the population from which the sample mean comes from is not normal, or unknown.

ASYMPTOTIC DISTRIBUTION- an estimator’s sampling distribution in large samples

ASYMPTOTIC PROPERTIES OF AN ESTIMATOR- properties of an estimator in large samples

Distribution Functions (Examples)

Below is a chart that shows a number of possible distribution functions and thier relationships.

Source

Video: Z-Scores

Standard Normal Table

See image below (Click to Enlarge)

Basic Demographics of #AgChat Facebook Group Members

Created using R and ‘members to .csv’ Facebook Ap
March 9, 2010


Breakdown by Gender (Click to Enlarge)



Representation by City and State

Augusta , Illinois
Chicago , Illinois
Indianapolis, Indiana
Hampton , Iowa
Miltonvale, Kansas
Louisville , Kentucky
Caneyville, Kentucky
Frankfort , Kentucky
Winnipeg, Manitoba (Canada)
Saginaw , Michigan
Deckerville, Michigan
Springfield , Missouri
Tecumseh, Oklahoma
Portland, Oregon
Fredrikstad , Ostfold (Norway)
Dallas ,Texas
Selah , Washington
Union West , Virginia

# of Members by State (Click to Enlarge)



Representation By Country (Click to Enlarge)
(Canada, Norway & the U.S.)



Notes:
Note:This data is for demonstration purposes only. There were actually 643 members of the #AgChat Facebook group as of this date, but the ‘members to .csv’ ap limits data retrieval to 499 observations, so this represents only a sampling of actual members. Observations are also omitted for missing values for variables in each respective analysis.For instance, only 24 observations of the available 499 had hometown data listed.

R Code for Sample Statistics Problesm

#################################################
# SELECTED PRACTICE PROBLEMS USING R -SCHAUMS
#################################################

# P.49-50

# 3.1
sales<-c(.10,.10,.25,.25,.25,.35,.40,.53,.90,1.25,1.35,2.45,2.71,3.09,4.10)

summary(sales)
sum(sales)

#3.5

salary<-c(240,240,240,240,240,240,240,240,255,255,265,265,280,280,290,300,305,325,330,340)

sum(salary)# just to check your work done by hand

summary(salary)


#---------------------------------
# EXAMPLE OF HISTOGRAM
#---------------------------------


library(lattice)# graphing package

hist(salary) # graph histogram

d <- density(salary) # fit curve to data

plot(d) # plot curve

# 4.9

minutes<-c(5,5,5,7,9,14,15,15,16,18)

print(minutes)

summary(minutes)

var(minutes)

sd(minutes)

library(lattice) # for graphics,but not necessary if previously loaded

hist(minutes)

d<-density(minutes)

plot(d)

#4.24

weights<-c(21,18,30,12,14,17,28,10,16,25)

sum(weights)

summary(weights)

sum(weights*weights) gives sum of X squared

var(weights)

sd(weights)


#4.33

cars<-c(2,4,7,10,10,10,12,12,14,15)

print(cars)

sum(cars)

summary(cars)

sum(cars*cars)

var(cars)

sd(cars)

(4.16866/9.6)*100 #co-efficient of variation

#################################################
# SELECTED PRACTICE PROBLEMS USING R -WILLIAMS
#################################################

#P.107

#1a

sample<-c(10,20,12,17,16)

print(sample)

summary(sample)

#2a

sample<-c(10,20,21,17,16,12)

print(sample)

summary(sample)

#p.151

#61

loans<-c(10.1,14.8,5,10.2,12.4,12.2,2,11.5,17.8,4)

print(loans)

sum(loans)

summary(loans)

sum(loans^2)

var(loans)

sd(loans)

#63

public<-c(28,29,32,37,33,25,29,32,41,34)

print(public)

sum(public)

summary(public)

sum(public^2)

var(public)

sd(public)

(4.64/32)*100 #CV

auto<-c(29,31,33,32,34,30,31,32,35,33)

print(auto)

sum(auto)

summary(auto)

sum(auto^2)

var(auto)

sd(auto)

(1.83/3.33)*100 #CV

Statistics References

I will post links related to statistics that might be useful as resources as you are learning statistics.

Handbook of Biological Statistics - Online stats textbook

NetMBA - Statistics

SatTrek

Standard Normal Table ( TAMU) (pdf)


t-table (1&2tailed) (image)

t-table (image)

Video: Z-scores

Distribution Functions

Data Sets -from Math Forum

Video- Regression Demo

Using R for Intro Statistics- John Veranzi

Animal Cruelty and Statistical Reasoning

In a recent article, animal rights activists (Mercy for Animals-MFA) went undercover and made some observations about animal abuse on dairy farms. See-
Governor Paterson, Shut This Dairy Down

The author of the above article states:

"But the grisly footage that every farm randomly chosen for investigation--MFA has investigated 11--seems to yield, indicates the violence is not isolated, not coincidental, but agribusiness-as-usual."

Where the statement above could get carried away, is if someone tried to apply it not only to the population of dairy farmers in that state or region, but to the industry as a whole. It's not clear how broadly they are using the term 'agribusiness as usual' but let's say a reader of the article wanted to apply it to the entire dairy industry.

This is exactly why economists and scientists employ statistical methods. Anyone can make outrageous claims about a number of policies, but are these claims really consistent with evidence? How do we determine if some claims are more valid than others?

Statistical inference is the process by which we take a sample and then try to make statements about the population based on what we observe from the sample. If we take a sample (like a sample of dairy farms) and make observations, the fact that our sample was 'random' doesn't necessarily make our conclusions about the population it came from valid.

Before we can say anything about the population, we need to know 'how rare is this sample?' We need to know something about our 'sampling distribution' to make these claims.

According to the USDA, in 2006 there were 75,000 dairy operations in the U.S. According to the activists claims, they 'randomly' sampled 11 dairies and found abuse on all of them. That represents just .0146% of all dairies. If we wanted to investigate the proportion of dairy farms that were abusing animals, if we wanted to be 90% confident in our estimate ( that is construct a 90% confidence interval) and we wanted the estimate (within the confidence interval)to be within a margin of error of .05, then the sample size required to estimate this proportion can be given by the following formula:

n = (z/2E)^2 where

z = value from the standard normal distribution associated with a 90% confidence interval

E = the margin of error

The sample size we would need is: (1.645/2*.05)^2 = (16.45)^2 = 270.65 ~271 farms!

To do this we have to make some assumptions:

Since we don't know the actual proportion of dairy farms that abuse animals, the most objective estimate may be 50%. The formula above is derived based on that assumption. (if we assumed 90% then it turns out based on the math (not shown) that the sample size would have to be the same as if we assumed that only 10% of farms abused their animals, which gives a sample size of about 98 or way more than 11). This also assumes normally distributed data. But to calculate anything, we would have to depend still on someone's subjective opinion of whether a farm was engaging in abuse or not.

I'm sure the article that I'm referring to above was never intended to be scientific, but the author should have chosen their words more carefully. What they have is allegedly a 'random' observation and nothing more. They have no 'empirical' evidence to infer from their 'random' samples that these abuses are 'agribusiness-as-usual' for the whole population of dairy farmers.

While MFA may have evidence sufficient for taking action against these individual dairies, the question becomes how high should the burden of proof be to support an increase in government oversight of the industry as a whole? (which seems to be the goal of many activist organizations)This kind of analysis involves consideration of the tradeoffs involved. This may depend partly on subjective views. We can use statistics to validate claims made on both sides of the debate, but statistical tests have no 'power' in weighing one person's preferences over another. Economics has no way to make interpersonal comparisons of utility.

Note: The University of Iowa has a great number of statistical calculators for doing these sorts of calculations. The sample size option can be found here. In the box, just select 'CI for one proportion' Deselect finite population ( since the population of dairies is quite large at 75,000)then select your level of confidence and margin of error.

References:

Profits, Costs, and the Changing Structure of Dairy Farming / ERR-47
Economic Research Service/USDA Link

"Governor Patterson Shut Down This Dairy", Jan 27,2010. OpEdNews.com

R Code for Basic Histograms

#####################################################
## THIS IS A LITTLE MORE STRAIGHT FORWARD THAN THE ##
## THE OTHER EXAMPLE- USING A SIMPLE DATA SET READ ##
## DIRECTLY FROM R VS. A FILE OR WEB ##
#####################################################

#----------------------------------------#
# SCHAUM'S P. 49 3.5 SALARY DATA
# BASIC HISTOGRAM
#----------------------------------------#


# LOAD SALARY DATA INTO VARIABLE SALARY

salary<-c(240,240,240,240,240,240,240,240,255,255,265,265,280,280,290,300,305,325,330,340) print(salary) # SEE IF IT IS CORRECT library(lattice) # LOAD THE REQUIRED lattice PACKAGE FOR GRAPHICS hist(salary) # PRODUCE THE HISTOGRAM # SEE OUTPUT BELOW

#---------------------------------------
# HISTOGRAM OPTIONS FOR COLOR ETC.
#----------------------------------------

hist(salary, breaks=6, col="blue") # MANIPULATE THE # OF BREAKS AND COLOR

# CHANGE TITLE AND X-AXIS LABEL

hist(salary, breaks=6, col="blue", xlab ="Weekly Salary", main ="Distribution of Salary")

#-------------------------------------------------
# FIT A SMOOTH CURVE TO THE DATA- KERNAL DENSITY
#-------------------------------------------------

d <- density(salary) # CREATE A DENSITY CURVE TO FIT THE DATA

plot(d) # PLOT THE CURVE

plot(d, main="Kernal Density Distribution of Salary") # ADD TITLE

polygon(d, col="yellow", border="blue") # ADD COLOR

R Code for Mean, Variance, and Standard Deviation

##################################################
## REMEMBER, THIS IS ONLY THOSE INTERESTED IN R
## YOU ARE NOT REQUIRED TO UNDERSTAND THIS CODE
## WE WILL WORK THROUGH THIS IN CLASS ON THE BOARD
## AND IN EXCEL
##################################################

#---------------------------------#
# DEMONSTRATE MEAN AND VARIANCE #
#---------------------------------#

###################################
# DATA: Corn Yields
#
# Garst: 148 150 152 146 154
#
# Pioneer: 150 175 120 140 165
###################################

# compute descriptive statistics for Garst corn yields

garst<-c(148, 150, 152, 146, 154) # enter values for 'garst'

print(garst) # see if the data is there

summary(garst) # this gives the mean, median, min, max Q1,Q3

var(garst) # compute variance

sd(garst) # compute standard deviation

plot(garst)


# compute descriptive statistics for Pioneer Corn Yields

pioneer<-c(150, 175, 120, 140, 165)

print(pioneer)

summary(pioneer)

var(pioneer)

sd(pioneer)

plot(pioneer)

APPLICATIONS USING R

While we will primarily rely on Excel to do your empirical projects and for examples in class, if you have an interest in programming, I encourage you to explore the free statistical programming language R.

The links below highlight applications of the R programming language. Some of these are far more advanced than what we will address in class, and some don't necessarily involve statistics-but I share them with you to illustrate how flexible the language can be for a number of things. Learning to use R for statistics is a great way to get started. If you are interested in learning more, please don't hesitate to contact me.

Visualizing Taxes and Deficits Using R and Google Visualization API

R in the New York Times

How to integrate R into web-based applications (video) using Rapache

Using Social Network Analysis to Analyze Tweets with R

Creating a Histogram in SAS

*---------------------------------------------------*
READ RAW DATA INTO SAS

ASSUMPTIONS:

1) DATA IS IN CSV FILE LOCATED ON YOUR DESKTOP NAMED
'hso.vsc'

*---------------------------------------------------*
;

PROC IMPORT OUT= WORK.HSO
DATAFILE= "C:\Documents and Settings\wkuuser\Desktop\hs0.csv"
DBMS=CSV REPLACE;
GETNAMES=YES;
DATAROW=2;
RUN;

*---------------------------------------*
CREATING A HISTOGRAM IN SAS
*---------------------------------------*
;

PROC UNIVARIATE DATA = HSO;
VAR WRITE;
HISTOGRAM WRITE;
TITLE ’HISTOGRAM OF THE HOS DATA’;
RUN;

SAS Links

UCLA SAS Links

SAS-R-Blog

R Statistical Software Links

Using R in the Real World

Why use R Statistical Software?

Google's R Style Guide - Set up for Google's corporate programmers


UCLA R Resources

Statistical Computing with R: A Tutorial (Illinois State University)

(UCLA R Class Notes) -great example code for getting started with R

Quick R (Statistics Guide)

R-Project ( Where you go to get R software Free)

SAS-R Blog

Using R for Introductory Statistics (John Verzani)

Creating a Histogram In R

# READ DATA SET CALLED 'hs0' from Web:

hs0 <- read.table("http://www.ats.ucla.edu/stat/R/notes/hs0.csv", header=T, sep=",")

attach(hs0)

# Or if you have downloaded the data set to your desktop:

hs0 <- read.table("C:\\Documents and Settings\\wkuuser\\Desktop\\hs0.csv", header=T, sep=",")

attach(hs0)


# print summary of first 20 observations to see what the data looks like

hs0[1:20, ]

# CREATE HISTOGRAM FOR VARIABLE 'write'

library(lattice)

hist(write)

Why use R Statistical Software

From: http://datamining.togaware.com/survivor/Pros_Cons.html


*R is the most comprehensive statistical analysis package available. It incorporates all of the standard statistical tests, models, analyses, as well as providing a comprehensive language for managing and manipulating data.

* R is a programming language and environment developed for statistical analysis by practising statisticians and researchers.

* R is developed by a core team of some 10 developers, including some of the worlds leading Statisticians.

* The validity of the R software is ensured through openly validated and comprehensive governance as documented for the American Food and Drug Authority in XXXX. Because R is open source, unlike commercial software, R has been reviewed by many internationally renowned statisticians and computational scientists.

* R has over 1400 packages available specialising in topics like from Econometrics, Data Mining, Spatial Analysis, Bio-Informatics.

* R is free and open source software allowing anyone to use and, importantly, to modify it. R is licensed under the GNU General Public License, with Copyright held by The R Foundation for Statistical Computing.

* Anyone can freely download and install the R software and even freely modify the software, or look at the code behind the software to learn how things are done.

* Anyone is welcome to provide bug fixes, code enhancements, and new packages, and the wealth of quality packages available for R is a testament to this approach to software development and sharing.

* R well integrates packages in different languages, including Java (hence the Rpackage[]RWeka package), Fortran (hence Rpackage[]randomForest), C (hence Rpackage[]arules), C++, and Python.

* The R command line is much more powerful than a graphical user interface.

* R is cross platform. R runs on many operating systems and different hardware. It is popularly used on GNU/Linux, Macintosh, and MW/Windows, running on both 32bit and 64bit processors.

* R has active user groups where questions can be asked and are often quickly responded to, and often responded to by the very people who have developed the environment--this support is second to none. Have you ever tried getting support from people who really know SAS or are core developers of SAS?

* New books for R (the Springer Use R! series) are emerging and there will soon be a very good library of books for using R.

* No license restrictions (other than ensuring our freedom to use it at our own discretion) and so you can run R anywhere and at any time.

* R probably has the most complete collection of statistical functions of any statistical or data mining package. New technology and ideas often appear first in R.

* The graphic capabilities of R are outstanding, providing a fully programmable graphics language which surpasses most other statistical and graphical packages.

* A very active email list, with some of the worlds leading statisticians actively responding, is available for anyone to join. Questions are quickly answered and the archive provides a wealth of user solutions and examples. Be sure to read the Posting Guide first.

* Being open source the R source code is peer reviewed, and anyone is welcome to review it and suggest improvements. Bugs are fixed very quickly. Consequently, R is a rock solid product. New packages provided with R do go through a life cycle, often beginning as somewhat less quality tools, but usually quickly evolving into top quality products.

* R plays well with many other tools, importing data, for example, from CSV files, SAS, and SPSS, or directly from MS/Excel, MS/Access, Oracle, MySQL, and SQLite. It can also produce graphics output in PDF, JPG, PNG, and SVG formats, and table output for LATEX and HTML.

EXAMPLE CODE

SAS CODE

Histogram


R CODE

NOTE: the code in these posts looks sloppy, but if you cut and paste into notepad or the R scripting window it lines up nice

Histogram

Histogram using Schaum's Homework Data (more straightforward than example above)

Kernal Density Plots -

R Code Mean, Variance, Standard Deviation

Selected Practice Problems for Test 1

Regression using R

Plotting Normal Curves and Calculating Probability

Statistics News and Industry

These applications are examples of statistics used in the real world. Many of them may involve more advanced concepts than what we will discuss in class, but my goal is to show you the numerous applications and possibilities with statistics. If you have any questions about anything posted here, don't hesitate to ask.

The new field of Data Science
Applications Using R
Statistics Summary For Media (humor)
For today's graduate just one word: Statistics
Animal Cruelty and Statistical Reasoning
Copulas and the Financial Crisis

Concepts from Mathematical Statistics

A. Concepts from Mathematical Statistics

Probability Density Functions

Random Variables

A random variable takes on values that have specific probabilities of occurring
( Nicholson,2002). An example of a random variable would be the number of car accidents per year among sixteen year olds.

If we know how random variables are distributed in a population, then we may have an idea of how rare an observation may be.

Example: How often sixteen year olds are involved in auto accidents in a year’s time.

This information is then useful for making inferences ( or drawing conclusions) about the population of random variables from sample data.

Example: We could look at a sample of data consisting of 1,000 sixteen year olds in the Midwest and make inferences or draw conclusions about the population consisting of all sixteen year olds in the Midwest.

In summary, it is important to be able to specify how a random variable is distributed. It enables us to gauge how rare an observation ( or sample) is and then gives us ground to make predictions, or inferences about the population.

Random variables can be discrete, that is observed in whole units as in counting numbers 1,2,3,4 etc. Random variables may also be continuous. In this case random variables can take on an infinite number of values. An example would be crop yields. Yields can be measured in bushels down to a fraction or decimal.

The distributions of discrete random variables can be presented in tabular form or with histograms. Probability is represented by the area of a ‘rectangle’ in a histogram
( Billingsly, 1993).

Distributions for continuous random variables cannot be represented in tabular format due to their characteristic of taking on an infinite number of values. They are better represented by a smooth curve defined by a function ( Billingsly, 1993). This function is referred to as a probability density function or p.d.f.

The p.d.f. gives the probability that a random variable ‘X’ takes on values in a narrow interval ‘dx’ ( Nicholson, 2002). This probability is equivalent to the area under the p.d.f. curve. This area can be described by the cumulative density function c.d.f. The c.d.f. gives the value of an integral involving the p.d.f.

Let f(x) be a p.d.f.

P( a <= X <= b ) = a b f(x) dx = F ( x )

This can be interpreted to mean that the probability that X is between the values of ‘a’ and ‘b’ is given by the integral of the p.d.f from ‘a’ to ‘b.’ This value can be given by the c.d.f. which is F ( x ). Those familiar with calculus know that F(x) is the anti-derivative of f(x).


Common p.d.f’s

Most students are familiar with using tables in the back of textbooks for normal, chi-square, t, and F distributions. These tables are generated by the p.d.f’s for these particular distributions. For example, if we make the assumption that the random variable X is normally distributed then its p.d.f. is specified as follows:

f(x)= 1 / (2 ) -1/2 e –1/2 (x - )2/

where X~ N (  )

In the beginning of this section I stated that it was important to be able to specify how a random variable is distributed. Through experience, statisticians have found that they are justified in modeling many random variables with these p.d.f.’s. Therefore, in many cases one can be justified in using one of these p.d.f.’s to determine how rare a sample observation is, and then to make inferences about the population. This is in fact what takes place when you look up values from the tables in the back of statistics textbooks.

Mathematical Expectation

The expected value E(X) for a discrete random variable can be defined as ‘the sum of products of each observation Xi and the probability of observing that particular value of Xi ( Billingsly, 1993). The expected value of an observation is the mean of a distribution of observations. It can be thought of conceptually as an average or weighted mean.

Example: given the p.d.f. for the discrete random variable X in tabular format.

Xi : 1 2 3

P(x =xi) .25 .50 .25


E (X) = Xi P(x =xi) = 1 * .25 + 2*.50 + 3*.25 = 2.0

Conceptually, the expected value of a random variable can be viewed as a point of balance or center of gravity. In reality, the actual value of an observed random variable will likely be larger or smaller than the ‘expected value.’ However due to the nature of the expected value, actual observations will have a distribution that is balanced around the expected value. For this reason the expected value can be viewed as the balancing point for a distribution, or the center of gravity ( Billingsly, 1993).

That is to say that population values cluster or gravitate around the expected value. Most of the population values are expected to be found within a small interval ( i.e. measured in standard deviations) about the population’s expected value or mean. Hence the expected values gives a hint about how rare a sample may be. Values lying near a population mean should not be rare but quite common.

The expected value for a continuous random variable must be calculated using integral calculus.

E(X) = ∫ x f(x) dx

If x is an observed value and f(x) is the p.d.f. for x, then the product x f(x) dx is the continuous version of the discrete case Xi P(x =xi) and integration is the continuous version of summation.

Variance

As I mentioned previously, actual observations will often depart from the expected value. Variance quantifies the degree to which observations in a distribution depart from an expected value. It is a mean of squared deviations between an observation and an expected value/mean (Billingsly, 1993).

In the discrete case we have the following mathematical description:

X -  )2 = 2

In the continuous case:

∫ (X -  )2 f(x) dx = E( X -  ) = 2


Given the mean (), or expected value of a random variable, one knows the value a random variable is likely to assume on average. The variance (2) indicates how close these observations are likely to be to the mean or expected value on average.




Sample Estimates

Given knowledge of the population mean and variance, one can characterize the population distribution for a random variable. As I mentioned at the beginning of the previous section, it is important to be able to specify how a random variable is distributed. It enables us to gauge how rare an observation ( or sample) is and then gives us grounds to make predictions, or inferences about the population.

It is not always the case that we have access to all of the data from a population necessary for determining population parameters like the mean and variance. In this case we must estimate these parameters using sample data to compute estimators or statistics.

Estimators or statistics are mathematical functions of sample data. The approach most students are familiar with in computing sample statistics is to compute the sample mean ( Xbar) and sample variance (s2) from sample data to estimate the population mean () and variance (2). This is referred to as the analogy principle, which involves using a corresponding sample feature to estimate a population feature (Bollinger,2002).


Properties of Estimators

A question seldom answered in many undergraduate statistics or research methods courses is how do we justify computing a sample mean from a small sample of observations, and then use it to make inferences about the population?

I have discussed the fact that most of the values in a population can be expected to be found within a small interval about the population mean or expected value. The question remains to be can we expect that most of the values of a population observation be found within a small interval of a sample mean? This must be true if we are to make inferences about the population using sample data and estimators like the sample mean.

Just like random variables, estimators or statistics have distributions. The distributions of estimators/statistics are referred to as sampling distributions. If the sampling distribution of a statistic is similar to that of the population then it may be useful to use that statistic to make inferences about the population. In that case sample means and variances may be good estimators for population means and variances.

Fortunately statisticians have developed criteria for evaluating ‘estimators’ like the sample mean and variance. There are four properties that characterize good estimators.




Unbiased Estimators

If ^ is an estimator for the population parameter , and if
E (^ then ^ is an unbiased estimator of the population parameter . This implies that the distribution of the sample statistic/estimator is centered around the population parameter ( Bollinger, 2002).

Consistency

^ is a consistant estimator of  if

lim as n infinity : Pr[ | ^ -  | < c ] = 1

This implies that as you add more and more data, the probability of getting closer and closer to  gets large or variance of ^ approaches zero as n approaches infinity. It can be said that ^ p  or converges in probability to  (Bollinger, 2002).

Efficiency

This is based on the variance of the sample statistic/estimator. Given the estimator ^, and an alternative estimator ~, ^ is more efficient given that

Variance(^) < Variance(

Mean Squared Error is a method of quantifying efficiency.

MSE = E [ [ - ^]2] = V(^) + E[ (E(^) - )]2 = variance + bias squared.

It can then be concluded that for an unbiased estimator the measure of efficiency reduces to the variance (Bollinger, 2002).

Robustness

Robustness is determined by how other properties ( i.e. unbiasedness,consistency,efficiency,) are affected by assumptions made
(Bollinger, 2002).

When sample statistics or estimators exhibit these four properties, statisticians feel that they can rely on these computations to estimate population parameters. It can be shown mathematically that the formulas used in computing the sample mean and variance meet these criteria.






Confidence Intervals

Confidence intervals are based on the sampling distributions of a sample statistic/estimator. Confidence intervals based on these distributions tell us what values an estimator ( ex: the sample mean) is likely to take, and how likely or rare the value is ( DeGroot, 2002). Confidence intervals are the basis for hypothesis testing.

Theoretical Confidence Interval

If we assume that our sample data is distributed normally, Xi ~ N (2) then it can be shown that the statistic

Z = ( Xbar - )2 / (2 / n)1/2 ~ N( 0, 1) Standard Normal Distribution ( Billingsly, 1993).

Given the probabilities represented by the standard normal distribution it can be shown as a matter of algebra that

Pr ( -1.96 <= Z <= 1.96) = .95

The value 1.96 is the qauntile of the standard normal distribution such that there is only a .025 or 2.5% chance that we will find a Z value greater than 1.96. Conversely there is only a 2.5% chance of finding a computed Z value less than –1.96
( Steele, 1997).

As a matter of algebra it can be shown that


Pr(Xbar - 1.96 (2 / n)1/2 <= <= Xbar + 1.96 (2 / n)1/2 ) = .95

( Goldberger, 1991).

This implies that 95% of the time we can be confident that the population mean will be 1.96 standard deviations from the sample mean. The interval above then represents a 95% confidence interval ( Bollinger, 2002).


The Central Limit Theorem –Asymptotic Results

The above confidence interval is referred to as a Theoretical confidence interval. It is theoretical because is based on knowledge of the population distribution being normal. According to the central limit theorem:

Given random sampling, E(X) = , V(X) = 2 , the Z- statistic Z = ( Xbar - )2 / (2 / n1/2) converges in distribution to N( 0,1). That is


( Xbar - )2 / (2 / n1/2) ~A N(0,1)

It can then be stated that the statistic is asymptotically distributed standard normal.
Asymptotic properties are characteristics that hold as the sample size becomes large or approaches infinity. The CLT holds regardless of how that sample data is distributed, hence there are no assumptions about normality necessary (DeGroot 2002).

Student’s t Distribution-Exact Results

A limitation of the central limit theorem is that it requires knowledge of the population variance. In many cases we use s2 to estimate 2 . Gosset, a brewer for Guiness in the 1800’s was interested in normally distributed data with small sample sizes. He found that using Z with s2 to estimate 2 did not work well with small samples. He wanted a statistic that relied on exact results vs. large sample asymptotics ( Steele, 1997).

Working under the name Student, he developed the t distribution, where

t = ( Xbar - )2 / (s2 / n)1/2 ~ t(n-1)


The t distribution is the ratio of a normally distributed variable and chi-square distributed variable ( DeGroot, 2002). It is important to note that the central limit theorem does not apply because we are using s2 instead of 2. Here we can rely on using the t-table for constructing confidence intervals and rely on exact results vs. the approximate or asymptotic results of the
CLT ( DeGroot, 2002).

More Asymptotics- Extending the CLT

Sometimes we don’t know the distribution of the data we are working with, or don’t feel comfortable making assumptions of normality. Usually we have to estimate 2 with s2 . In this case we can’t rely on the asymptotic results of the CLT or the exact results of the t-distribution.

In this case there are some powerful theorems regarding asymptotic properties of sample statistics known as the Slutsky Theorems.